By

文章目录
  1. 1. 1. 概述
  2. 2. 2. 树状数组的结构
  3. 3. 3. 代码实现
  4. 4. 4. 参考资料

1. 概述

树状数组(BIT ,binary indexed tree)是一种查询和修改的时间复杂度都为log(n)的数据结构。传统的数组连续元素求和的时间复杂度为O(n),而树状数组通过将线性结构转换成伪树状结构，将复杂度降为log(n)。

2. 树状数组的结构

给定数组A,我们定义数组C，满足C[i]=A[i-2^k+1]+…+A[i],其中k为i转成二进制后末尾的0的个数，i从1开始计算，则我们称C为树状数组。其中2^k = i&(i^(i-1)),即i与i-1做异或运算再与i做与运算。

数组C的具体含义如下图所示：

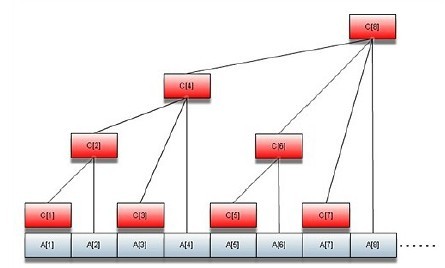
C[1]=A[1];
C[2]=A[1]+A[2];
C[3]=A[3];
C[4]=A[1]+A[2]+A[3]+A[4];
…
C[7]=A[7];
C[8]=A[1]+…+A[8];
分析上面的几组式子可知，当i为奇数时，C[i]=A[i] ；当i为偶数时，就要看i的因子中最多有二的多少次幂。例如，6的因子中有2的一次幂，等于2，所以C[6]=A[5]+A[6]（由六向前数两个数的和），4的因子中有2的两次幂，等于4，所以C[4]=A[1]+A[2]+A[3]+A[4]（由四向前数四个数的和） 。当我们修改A[i]的值时，只需要沿着C[i]往跟结点上溯，修改这条路上的所有结点即可，这种操作最坏情况下的时间复杂度为树的高度即log(n)，比线性结构的数组的复杂度O(n)快。

3. 代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//求2^k
int lowbit(int t)
{
	return t & ( t ^ ( t - 1 ) );
}
//求前n项和
//求出来 2^k 之后，数组C的值就都出来了
int sum(int n)
{
   int sum = 0;
   while(n > 0)
  {
	 sum += C[n];
	 n -= lowbit(n);
  }
  return sum;
}
 
//给某个节点pos加上num
void plus(int pos, int num)
{
   while(pos <= n)
  {
	 C[pos] += num;
	 pos += lowbit(pos);
  }
}

4. 参考资料

[1]. http://hawstein.com/posts/binary-indexed-trees.html
[2]. http://dongxicheng.org/structure/binary_indexed_tree/
[3]. http://www.cnblogs.com/zhangshu/archive/2011/08/16/2141396.html

文章目录
  1. 1. 1. 概述
  2. 2. 2. 树状数组的结构
  3. 3. 3. 代码实现
  4. 4. 4. 参考资料